728x90
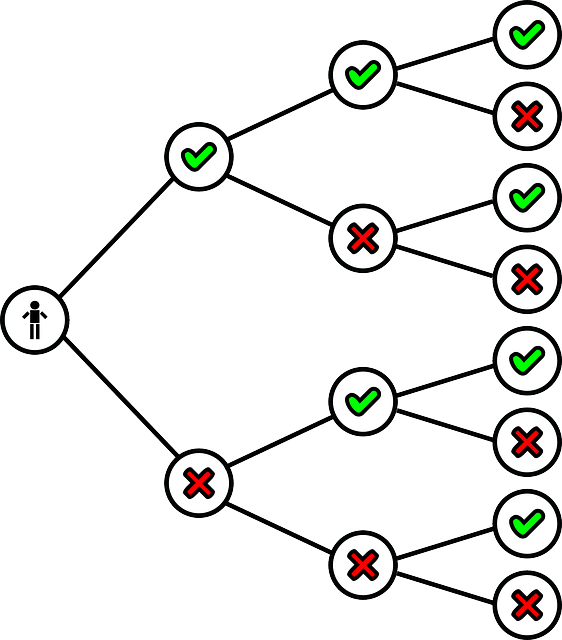
1. 이진탐색(Binary Search)란?
탐색할 자료를 둘로 나누어 해당 데이터가 있을 만한 곳을 탐색하는 방법
문제 : 1-30번째 병뚜껑에 각각 1~100 사이의 번호가 표시되어 있다. 이중에 70이 있을지 없을지 확인하는 방법은?
조건
1) 가장 적게 병을 따야 한다.
2) 각 병뚜껑에 쓰여진 번호는 낮은 번호 순으로 기입되어 있다.
방법 : 가운데 있는 병뚜껑을 순차적으로 따서 범위를 좁힌다.
이것이 이진탐색방법이다.
순차탐색 : index 0 부터 하나씩 찾기 때문에 훨씬 느리다.
2. 분할정복알고리즘과 이진탐색
- 분할정복 알고리즘
- Divide : 문제를 하나 또는 둘 이상으로 나눈다.
- Conquer : 나눠진 문제가 충분히 작고, 해결이 가능하다면 해결하고, 그렇지 않다면 다시 나눈다.
- 이진탐색
- Divide : 리스트를 두개의 서브리스트로 나눈다.
- Conquer
- 검색할 숫자(search)가 중간값보다 크면 뒷부분의 서브리스트에서 검색할 숫자를 찾는다.
- 검색할 숫자(search)가 중간값보다 작으면 앞부분의 서브리스트에서 검색할 숫자를 찾는다.
3. 알고리즘구현
- 이진 탐색은 데이터가 정렬되어 있는 상태에서 진행되는 탐색이다.
def binary_search(data,search) :
print(data)
if len(data)==1 and search ==data[0] :
return True
elif len(data)==1 and search!= data[0] :
return False
elif len(data) ==0 :
return False
medium = len(data)//2
if search == data[medium] :
return True
else :
if search>data[medium] :
return binary_search(data[medium:],search)
else :
return binary_search(data[:medium],search)import random
data_list=random.sample(range(100),10)
data_list.sort()data_list.sort()의 값은 다음과 같다.
[3, 19, 23, 27, 35, 39, 49, 74, 90, 96]탐색을 하기 위한 코드에서 데이터리스트에 없는 숫자를 입력한다.
binary_search(data_list,1)[3, 19, 23, 27, 35, 39, 49, 74, 90, 96]
[3, 19, 23, 27, 35]
[3, 19]
[3]
Out[59]:
False이와 같이 나온다.
데이터리스트에 있는 숫자를 입력한다.
binary_search(data_list,27)[3, 19, 23, 27, 35, 39, 49, 74, 90, 96]
[3, 19, 23, 27, 35]
[23, 27, 35]
Out[61]:
True
시간복잡도
- n개의 리스트를 2로 나누어 1이 될때 까지 비교연산을 k회 진행한다.
- 이를 식으로 나타내면 nx(1/2)^k =1 이다. 따라서 k=logn(밑은2).
- 따라서 이진탐색의 시간복잡도는 O(logn)
cf) 순차탐색
- 데이터가 담겨있는 리스트를 앞에서부터 하나씩 비교해서 원하는 데이터를 찾는 방법
문제1) 랜덤 데이터 리스트에서 원하는 데이터의 위치를 return하는 순차탐색 알고리즘을 작성해보자.
from random import*
rand_data_list=[]
for num in range(10) :
rand_data_list.append(randint(1,100))
def sequencial(data_list, search_data) :
for i in data_list :
if i==search_data :
return data_list.index(i)
return -1rand_data_list[48, 99, 66, 72, 79, 48, 93, 72, 43, 36]
데이터리스트에 있는 숫자를 입력하면 인덱스 번호가 출력된다.
sequencial(rand_data_list,72)3
데이터리스트에 없는 숫자를 입력하면 -1이 출력된다.
sequencial(rand_data_list,3)-1
시간복잡도
- 앞에서부터 순차적으로 탐색하기 때문에 최악의 경우는 당연히 O(n)이다.
'프로그래밍 > Python 알고리즘' 카테고리의 다른 글
| 10. 알고리즘 너비 우선 탐색, 깊이 우선 탐색 (0) | 2023.02.03 |
|---|---|
| 9. 알고리즘 그래프(Graph)와 자료구조 (0) | 2023.01.26 |
| 7. 알고리즘 정렬 병합정렬(merge sort) (0) | 2023.01.26 |
| 6. 알고리즘 퀵 정렬 (quick sort) (0) | 2023.01.25 |
| 5. 알고리즘 동적계획법(dynamic programming)과 분할정복 (1) | 2023.01.25 |




댓글